केशिकात्व, केशनली क्या है, सूत्र, कारण | capillarity in Hindi class 11

केशिकात्व

केशनली में द्रव के ऊपर चढ़ने तथा नीचे उतरने की घटना को केशिकात्व (capillarity in Hindi) कहते हैं। केशिकात्व का कारण पृष्ठ तनाव है।

दोनों तरफ से खुली केश (बालों) के समान बारीक छिद्र वाली नली को केशनली कहते हैं।

केशिकात्व का कारण

केशिकात्व का कारण पृष्ठ तनाव है।

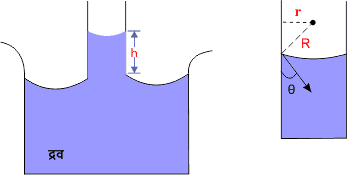
जब केशनली को जल में खड़ा किया जाता है तो केशनली में के भीतर अवतल पृष्ठ के नीचे का दाब कम हो जाता है। अतः दाब की इस कमी को पूरा करने के लिए जल केशनली में ऊपर चढ़ने लगता है। और एक निश्चित ऊंचाई पर जाकर रुक जाता है। इस स्थिति में h ऊंचाई के जल स्तंभ, दाब 2T/R के बराबर होता है अर्थात

hρg = \frac{2T}{R}
यदि केशनली तथा जल के बीच स्पर्श कोण θ है तो
R = \frac{r}{cosθ}
अतः   hρg = \frac{2T}{r/cosθ}
hρg = \frac{2Tcosθ}{r}
\footnotesize \boxed { h = \frac{2Tcosθ}{rρg} }

अतः इस समीकरण द्वारा स्पष्ट होता है कि
(i) r, ρ, g, θ का मान कम तथा T का मान अधिक होने पर h का मान अधिक होगा।
(ii) यदि θ > 90° है तो cosθ के ऋणात्मक होने के कारण h ऋणात्मक हो जाएगा अर्थात द्रव केशनली से नीचे उतर जाएगा।

पढ़ें… 11वीं भौतिक नोट्स | 11th class physics notes in Hindi

केशनली में द्रव के उन्नयन का निगमन

माना कांच की r त्रिज्या की एक नली है जो द्रव (जल) में खड़ी है। जिसका पृष्ठ तनाव T है केशनली में द्रव h ऊंचाई तक चढ़ जाता है। द्रव तथा कांच के लिए स्पर्श कोण θ है। पृष्ठ तनाव T को हम दो घटकों में वियोजित कर सकते हैं।

साम्यावस्था में
ऊपर की ओर लगने वाला बल
F = h ऊंचाई के जल स्तंभ का भार
2πr × Tcosθ = πr²hρg
2Tcosθ = rhρg
\footnotesize \boxed { h = \frac{2Tcosθ}{rρg} }
या \footnotesize \boxed { T = \frac{rhρg}{2cosθ} }

Note –
ताप बढ़ाने पर पृष्ठ तनाव का मान घट जाता है तथा क्रांतिक ताप पर इसका मान शून्य होता है।