द्रव्यमान केंद्र किसे कहते हैं परिभाषा, सूत्र | किसी निकाय के संहति केंद्र की गति

द्रव्यमान केंद्र

जब निकाय किसी बाह्य बल के अंतर्गत गति करता है तब उसका कोई बिंदु इस प्रकार गति करता है कि जैसे निकाय का समस्त द्रव्यमान इस बिंदु पर केंद्रित हो तथा बाह्य बल भी इसी बिंदु पर आरोपित हो, तो इस बिंदु को निकाय का द्रव्यमान केंद्र (centre of mass in Hindi) कहते हैं। इसे C द्वारा प्रदर्शित किया जाता है यही द्रव्यमान केंद्र की परिभाषा है।

ध्यान दें
NCERT book में संहति केंद्र प्रयोग किया गया है संहति केंद्र और द्रव्यमान केंद्र एक ही चीज है। इसे दोनों में से किसी भी नाम से लिख सकते हैं।

दो कणों के निकाय का द्रव्यमान केंद्र

माना दो कण जिनका द्रव्यमान m₁ व m₂ है जिन्हें चित्र में बिंदुओं से दर्शाया गया हैं। यह दोनों कण एक ही निकाय में स्थित है।

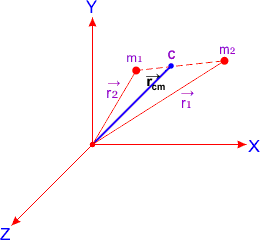
मूलबिंदु O के सापेक्ष कणों के स्थिति सदिश क्रमशः \small \overrightarrow{r_1} व \small \overrightarrow{r_2} हैं यदि निकाय का द्रव्यमान केंद्र C है तो इसका स्थिति सदिश निम्न होगा।
\footnotesize \boxed { \overrightarrow{r_{cm}} = \frac{m_1\overrightarrow{r_1} + m_2\overrightarrow{r_2}}{m_1 + m_2} }
cm का मतलब centre of mass (द्रव्यमान केंद्र) है।

NOTE
यदि निकाय में दो कण की जगह अनेक कण हैं तो निकाय का स्थिति सदिश निम्न होगा।
\footnotesize \boxed { \overrightarrow{r_{cm}} = \frac{1}{M} \int \overrightarrow{r}\,dm }
जहां M निकाय का संपूर्ण द्रव्यमान तथा dm सूक्ष्म अवयव का द्रव्यमान है एवं \overrightarrow{r} इसका स्थिति सदिश है।

पढ़ें… 11वीं भौतिक नोट्स | 11th class physics notes in Hindi

द्रव्यमान केंद्र की गति

माना कोई निकाय जिसमें n कण हैं। जिसके द्रव्यमान क्रमशः m₁, m₂, m₃…… m_n हैं यदि मूलबिंदु के सापेक्ष इनके स्थिति सदिश क्रमशः \small \overrightarrow{r_1} , \small \overrightarrow{r_2} , \small \overrightarrow{r_3} …….. \small \overrightarrow{r_ n} हैं
तब निकाय के द्रव्यमान केंद्र का स्थिति सदिश
\small \overrightarrow{r_{cm}} = \large \frac{m_1\overrightarrow{r_1} + m_2\overrightarrow{r_2} + …….m_n\overrightarrow{r_n}}{m_1 + m_2 + ……..m_n}
\small \overrightarrow{r_{cm}} = \frac{1}{M}(m_1\overrightarrow{r_1} + m_2\overrightarrow{r_2} + …….m_n\overrightarrow{r_n})
जहां M निकाय का कुल द्रव्यमान है
कुल द्रव्यमान का समय के साथ अवकलन करने पर
\large \frac{\overrightarrow{r_{cm}}}{dt} = \frac{1}{M} (m_1\frac{\overrightarrow{r_1}}{dt} + m_2\frac{\overrightarrow{r_2}}{dt} +…….m_n\frac{\overrightarrow{r_n}}{dt})
चूंकि वेग = दूरी/समय होता है तब
\footnotesize \boxed { \overrightarrow{v_cm} = \frac{1}{M} (m_1\overrightarrow{v_1} + m_2\overrightarrow{v_2} +…….m_n\overrightarrow{v_n}) }
जहां \overrightarrow{v_cm} द्रव्यमान केंद्र का कुल वेग है।

यदि निकाय पर कार्यरत कुल बाह्य बल \footnotesize \overrightarrow{F_{ext}} हो तब
\footnotesize \boxed { \overrightarrow{F_{ext}} = M \overrightarrow{a_{cm}} }
जहां \small \overrightarrow{a_{cm}} निकाय के द्रव्यमान केंद्र का त्वरण है।

विलगित निकाय

वह निकाय जिस पर कार्यरत समस्त बाह्य बल शून्य हो, तो उस निकाय को विलगित निकाय (isolated system) कहते हैं। इसमें निकाय के द्रव्यमान केंद्र का वेग \small \overrightarrow{v_{cm}} नियत रहता है चूंकि \footnotesize \overrightarrow{F_{ext}} = 0
तब \small \overrightarrow{a_{cm}} = 0
अतः \footnotesize \boxed { \overrightarrow{v_{cm}} = नियतांक }