विद्युत द्विध्रुव क्या है इसके कारण विद्युत क्षेत्र की तीव्रता का व्यंजन, सूत्र

प्रस्तुत लेख के अंतर्गत विद्युत द्विध्रुव क्या है मात्रक, सूत्र एवं इसके कारण विद्युत क्षेत्र की तीव्रता का व्यंजन की अक्षीय स्थिति और निरक्षीय का व्यंजन प्राप्त करेंगे।

विद्युत द्विध्रुव

विद्युत द्विध्रुव एक ऐसा समायोजन है। जिसमें दो बराबर व विपरीत प्रकृति के आवेश एक दूसरे से अल्प दूरी पर होते हैं।

किसी एक (+q या -q) आवेश तथा दोनों आवेशों के बीच की दूरी (2l) के गुणनफल को विद्युत द्विध्रुव आघूर्ण कहते हैं। इसे p से प्रदर्शित करते हैं।
विद्युत द्विध्रुव का आघूर्ण p = आवेश × बीच की दूरी
p = q × 2l

p = 2ql

विद्युत द्विध्रुव का मात्रक कूलाम-मीटर होता है। तथा विमीय सूत्र [LTA] होता है। विद्युत द्विध्रुव एक सदिश राशि है। जिसकी दिशा ऋणात्मक आवेश (-q) से धनात्मक आवेश(+q) की ओर होती है।
विद्युत द्विध्रुव के उदाहरण – अनेक अणु जैसे HCl, H₂O, HBr, NH₃ तथा CH₄ वैद्युत द्विध्रुव के उदाहरण हैं।

विद्युत द्विध्रुव के कारण विद्युत क्षेत्र की तीव्रता

वैद्युत द्विध्रुव के कारण विद्युत क्षेत्र की तीव्रता ज्ञात करने की दो स्थितियां हैं।
1. अक्षीय स्थिति
2. निरक्षीय स्थिति

1. विद्युत द्विध्रुव के कारण विद्युत क्षेत्र की तीव्रता की अक्षीय या अक्ष स्थिति

अक्षीय स्थिति – माना एक वैद्युत द्विध्रुव AB ऐसे माध्यम के स्थित है। जिसका परावैघुतांक k है। अक्षीय स्थिति में इसके मध्य बिंदु O से r दूरी पर एक बिंदु P है। जिस पर विद्युत क्षेत्र के तीव्रता ज्ञात करनी है।

( Note – ये जो ऊपर परिभाषा लिखी गई है। यह चित्र से बनाई गई है। आप भी इसे रटे नहीं बल्कि चित्र को समझें, और बार-बार लिखने का अभ्यास करें।)

द्विध्रुव के आवेश +q के कारण बिंदु P पर विद्युत क्षेत्र की तीव्रता

इसी प्रकार द्विध्रुव के आवेश -q के कारण बिंदु p पर वैद्युत क्षेत्र की तीव्रता

(चूंकि तीव्रता एक सदिश राशि है। इसलिए ही -q आवेश भी +q हो जाता है)

E₁ व E₂ विपरीत दिशाओं मैं होने के कारण बिंदु O पर परिणामी तीव्रता

वायु अथवा निर्वात के लिए k = 1

इस प्रकार अक्षीय स्थिति में वैद्युत क्षेत्र की तीव्रता E की दिशा ऋण आवेश से धन आवेश की ओर होती है।

पढ़ें… 12वीं भौतिकी नोट्स | class 12 physics notes in hindi pdf

2. विद्युत द्विध्रुव के कारण विद्युत क्षेत्र की तीव्रता की निरक्षीय या निरक्ष स्थिति

निरक्षीय या निरक्ष स्थिति – माना एक वैद्युत द्विध्रुव AB ऐसे माध्यम के स्थित है। जिसका परावैघुतांक k है। निरक्षीय स्थिति में इसके मध्य बिंदु O से r दूरी पर एक बिंदु P है। जिस पर विद्युत क्षेत्र के तीव्रता ज्ञात करनी है।

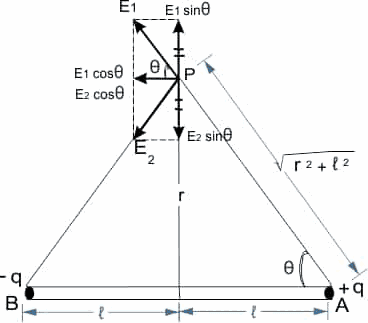
द्विध्रुव के आवेश +q के कारण बिंदु P पर विद्युत क्षेत्र की तीव्रता

इसी प्रकार द्विध्रुव के आवेश -q के कारण बिंदु p पर विद्युत क्षेत्र की तीव्रता

E₁ व E₂ को क्षैतिज व ऊर्ध्वाधर घटकों में नियोजित करने पर ऊर्ध्वाधर घटक E₁sinθ तथा E₂sinθ बराबर व विपरीत होने पर निरस्त (खत्म) हो जाते हैं। जबकि क्षैतिज घटक E₁cosθ तथा E₂cosθ एक ही दिशा में होने के कारण जुड़ जाएंगे।
अतः बिंदु P पर परिणामी तीव्रता

वायु अथवा निर्वात के लिए k=1

इस प्रकार निरक्षीय स्थिति में वैद्युत क्षेत्र की तीव्रता E की दिशा धन आवेश से ऋण आवेश की ओर होती है।

Note – 12th Physics Board Exam में इन दो स्थितियों में से कोई एक स्थिति आने की संभावना बहुत ज्यादा होती है। इसलिए आप इन्हें अच्छे से समझे और लिखकर अभ्यास करें।

एकसमान विद्युत क्षेत्र में स्थित द्विध्रुव पर लगने वाले बल युग्म के आघूर्ण

माना एक वैद्युत द्विध्रुव AB एक समान वैद्युत क्षेत्र E में क्षेत्र से कोण बनाते हुए रखा गया है। इस स्थिति में इसके +q आवेश पर एक बल F ( = qE) क्षेत्र की दिशा में तथा -q आवेश पर उतना ही बल F ( = qE) क्षेत्र की विपरीत दिशा में लगता है। अतः यह बल एक युग्म बनाते हैं।

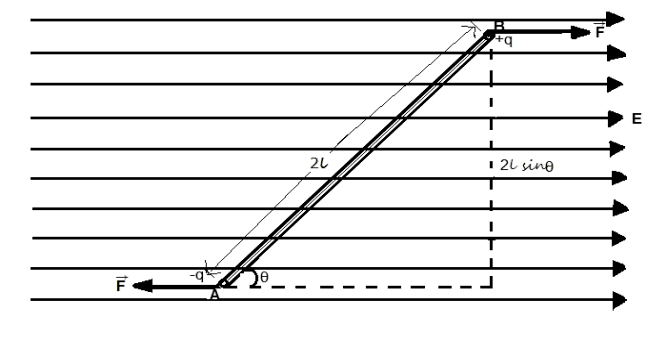
जो द्विध्रुव को वैद्युत क्षेत्र (E) के समांतर लाने का प्रयत्न करते हैं। अतः इसे प्रत्यानयन बल कहते हैं। इस प्रत्यानयन बल युग्म का आघूर्ण

τ = बल × लंबवत दूरी

विद्युत द्विध्रुव संबंधित प्रश्न उत्तर

---