प्रक्षेप्य गति किसे कहते हैं, परिभाषा, सूत्र, उड्डयन काल, पथ परवलयाकार होता है

प्रक्षेप्य गति किसे कहते हैं, प्रक्षेप्य गति की परिभाषा, सूत्र, उड्डयन काल, प्रक्षेप्य का पथ परवलयाकार होता है।

प्रक्षेप्य गति

जब किसी वस्तु को पृथ्वी के गुरुत्वीय क्षेत्र में एक प्रारंभिक वेग से किसी कोण पर फेंका जाता है तो वस्तु ऊर्ध्वाधर दिशा में लगते हुए गुरुत्वीय त्वरण के अंतर्गत एक वक्र पथ पर गति करती है। वस्तु की इस गति को प्रक्षेप्य गति (motion of a projectile in Hindi) कहते हैं। एवं वस्तु जिस पथ पर गति करती है उसे प्रक्षेप पथ कहते हैं।

प्रक्षेप्य गति के उदाहरण

1. तोप से छूटे गोले की गति
2. भाला फेंक खेल में भोले की गति
3. छत से फेंकी गई गेंद की गति
4. बल्लेबाज द्वारा मारी गई गेंद की गति
5. फुटबॉल खेल में गेंद की गति

प्रक्षेप्य का पथ

एक बहुत महत्वपूर्ण प्रश्न है कि सिद्ध कीजिए कि प्रक्षेप्य का पथ परवलयाकार होता है। यह हर साल exam में आता है पूरा निगमन करना होता है जो नीचे दिया गया है –

माना बिंदु O किसी पिंड को क्षैतिज से θ कोण पर प्रारंभिक वेग u से फेंका जाता है। चित्र में OX क्षैतिज रेखा है एवं OY ऊर्ध्वाधर रेखा है। प्रारंभिक वेग u को क्षैतिज व ऊर्ध्वाधर घटकों में विभाजित करने पर
क्षैतिज घटक u_x = ucosθ , गुरुत्वीय त्वरण a_x = 0
ऊर्ध्वाधर घटक u_y = usinθ , गुरुत्वीय त्वरण a_y = -g

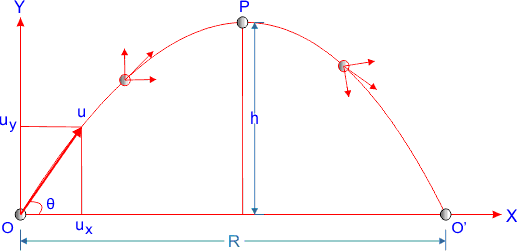
जैसे पीछे पढ़ा है कि पिंड की गति गुरुत्वीय त्वरण g के अंतर्गत है इसलिए यह त्वरण नीचे की ओर लगता है।
t समय पश्चात पिंड का क्षैतिज दिशा में विस्थापन
(गति के द्वितीय समीकरण s = ut + \large \frac{1}{2} at² से)
x = u_xt + \large \frac{1}{2} a_xt²
u_x = ucosθ , a_x = 0 रखने पर
x = ucosθt + \large \frac{1}{2} 0 × t²
x = ucosθt
या t = \large \frac{x}{ucosθ} समी.①
अब ऊर्ध्वाधर दिशा में विस्थापन
(गति के द्वितीय समीकरण s = ut + \large \frac{1}{2} at² से)
y = u_yt + \large \frac{1}{2} a_yt²
u_y = usinθ , a_y = -g रखने पर
y = usinθt + \large \frac{1}{2} × -g × t²
y = usinθt – \large \frac{1}{2} gt² समी.②
अब समी.① से t का मान समी.② में रखने पर
y = usinθ × \large \frac{x}{ucosθ} – \large \frac{1}{2} g( \large \frac{x}{ucosθ} )²
y = \large \frac{sinθ}{cosθ} × x – \large \frac{1}{2} g( \large \frac{x^2}{u^2cos^2θ}
\footnotesize \boxed { y = tanθx - (\frac{g}{2u^2cos^2θ}) x^2 }
यह समीकरण y = bx -cx² द्विघात समीकरण के समरूप है। जो परवलय को प्रदर्शित करता है अतः प्रक्षेप्य का पथ परवलयाकार होता है।

प्रक्षेप्य पर उड्डयन काल

जब किसी पिंड को वायु में फेंका जाता है तो फेंकने के बाद यह एवं जमीन पर गिरने से पहले अर्थात जितने समय तक पिंड वायु में रहता है उस समय को प्रक्षेप्य पर उड्डयन काल (flight time of projectile in Hindi) कहते हैं। इसे T द्वारा प्रदर्शित करते हैं।

गति के समीकरण v_y = u_y + a_yt
चूंकि पिंड वायु में है इसलिए अंतिम वेग v_y = 0 एवं v_y = usinθ , a_y = -g होगा अतः
0 = usinθ – gt
t = \large \frac{usinθ}{g}
यह समय पिंड के बिंदु O से बिंदु P तक पहुंचने का है अतः पूरे पिंड का उड्डयन काल इस समय का दोगुना होगा तब
\footnotesize \boxed { T = 2t = \frac{2usinθ}{g} }

प्रक्षेप्य की परास

पिंड को फेंकने से पिंड के गिरने तक की दूरी अर्थात् बिंदु O से बिंदु O’ तक की दूरी को प्रक्षेप्य की परास (range of projectile in Hindi) कहते हैं। इसे R द्वारा प्रदर्शित करते हैं।

क्षैतिज परास R = क्षैतिज वेग × उड्डयन काल
R = ucosθ × \large \frac{2usinθ}{g}
R = \large \frac{u^22sinθ.cosθ}{g}
चूंकि 2sinθ.cosθ = sin2θ होता है इसलिए
\footnotesize \boxed { R = \frac{u^2sin2θ}{g} }

पढ़ें… 11वीं भौतिक नोट्स | 11th class physics notes in Hindi

प्रक्षेप्य की ऊंचाई

प्रक्षेप्य गति में पिंड जितनी अधिकतम ऊंचाई प्राप्त करता है उसे प्रक्षेप्य की ऊंचाई (height of projectile in Hindi) कहते हैं। इसे h द्वारा प्रदर्शित करते हैं।
गति के तृतीय समीकरण v^2 = u^2 + 2as से
v = o , u = usinθ
0 = u²sin²θ + 2gh
\footnotesize \boxed { h = \frac{u^2sin^2θ}{2g} }

प्रक्षेप्य गति संबंधित प्रश्न-उत्तर

आशा है कि प्रक्षेप्य गति के सभी बिंदु आपको पसंद आए होंगे। अगर किसी टॉपिक से related आपका कोई प्रश्न है तो आप हमें comments से बता सकते हैं। प्रक्षेप्य का पथ परवलयाकार होता है इसकी तैयारी अच्छे से करें।