चतुष्फलकीय रिक्ति एवं अष्टफलकीय रिक्तियां क्या है, अंतर, परिभाषा

क्रिस्टल जालक संघन संकुलित होते हैं। लेकिन फिर भी गोलों के मध्य कुछ रिक्त स्थान रह जाता है। जिसे छिद्र अथवा रिक्ति कहते हैं।

त्रिकोणीय रिक्ति

तीन गोलों के निविड संकुलन में परस्पर स्पर्श करने पर उनके केंद्र एक समबाहु त्रिभुज के किनारों पर होते हैं। जिससे केंद्र के मध्य एक रिक्त स्थान रह जाता है जो समबाहु त्रिभुज के केंद्र पर होता है। इस रिक्त स्थान को ही त्रिकोणीय छिद्र या त्रिकोणीय रिक्ति कहते हैं।

घटक कणों के त्रिविमीय संवृत संकुलन में दो प्रकार की रिक्तियां पाई जाती है।
(1) चतुष्फलकीय रिक्ति
(2) अष्टफलकीय रिक्ति

1. चतुष्फलकीय रिक्ति

जब द्वितीय परत का एक गोला प्रथम परत के तीन गोलों के मध्य त्रिकोणीय रिक्ति के ऊपर होता है। तो एक नई रिक्ति का निर्माण होता है जिसे चतुष्फलकीय रिक्ति (tetrahedral voids in Hindi) कहते हैं।
ये चारों गोले एक चतुष्फलकीय रिक्ति का निर्माण करते हैं। आसान भाषा में कहें तो, चार स्पर्शी गोलों के मध्य स्थित रिक्ति को चतुष्फलकीय रिक्ति कहते हैं।

चतुष्फलकीय रिक्ति की संख्या संकुलन में परमाणुओं की संख्या के दोगुनी होती है। अर्थात्
चतुष्फलकीय रिक्ति की संख्या = 2 × संकुलन में परमाणुओं की संख्या (6.022 × 10²³)
चतुष्फलकीय रिक्ति की त्रिज्या r तथा घटक कण की त्रिज्या R में निम्न संबंध होता है।
\footnotesize \boxed { r = 0.225 R }
अर्थात् चतुष्फलकीय रिक्ति की त्रिज्या, घटक कण की त्रिज्या के 0.225 गुनी होती है।

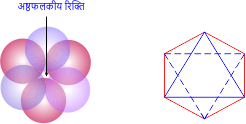
2. अष्टफलकीय रिक्ति

इस रिक्ति का निर्माण दो त्रिकोणीय रिक्तियों के संयोग से होता है। अर्थात् एक परत की त्रिकोणीय रिक्ति के ऊपर दूसरी परत की त्रिकोणीय रिक्ति को विपरीत दशा में रखा जाता है। तो एक नई रिक्ति का निर्माण होता है। जिसे अष्टफलकीय रिक्ति (octahedral voids in Hindi) कहते हैं।
अष्टफलकीय रिक्ति का निर्माण 6 गोलाकार कणों से होता है।
आसान शब्दों में – छः गोलों के मध्य स्थित रिक्ति को अष्टफलकीय रिक्ति कहते हैं।

अष्टफलकीय रिक्ति की संख्या संकुलन में परमाणुओं की संख्या के बराबर होती है। अर्थात्
अष्टफलकीय रिक्ति की संख्या = संकुलन में परमाणुओं की संख्या (6.022 × 10²³)
अष्टफलकीय रिक्ति की त्रिज्या r तथा घटक कण की त्रिज्या R में निम्न संबंध होता है। अतः
\footnotesize \boxed { r = 0.414 R }
अर्थात् अष्टफलकीय रिक्ति की त्रिज्या, घटक कण की त्रिज्या के 0.414 गुनी होती है।

Note –
अष्टफलकीय रिक्तियों की संख्या N, चतुष्फलकीय रिक्तियों की संख्या n की दोगुनी होती है। अतः
\footnotesize \boxed { N = 2n }