जड़त्व आघूर्ण क्या है इसके बारे में हम पूरी जानकारी पिछले अध्याय में प्राप्त कर चुके हैं उसमें हमने जड़त्व आघूर्ण तथा घूर्णन त्रिज्या के बारे में भी संपूर्ण अध्ययन किया है। इस अध्याय में जड़त्व आघूर्ण संबंधी समांतर व लम्ब अक्षों की प्रमेय को सिद्ध कीजिए इसे सरल भाषा में विस्तार से अध्ययन करेंगे।
जड़त्व आघूर्ण संबंधी प्रमेय
जड़त्व आघूर्ण संबंधी प्रमेय दो प्रकार की होती हैं-
(1) समांतर अक्षों की प्रमेय
(2) लम्ब अक्षों की प्रमेय
1. समांतर अक्षों की प्रमेय
किसी पिंड का किसी घूर्णन अक्ष के परितः जड़त्व आघूर्ण (I), उस पिंड के द्रव्यमान केंद्र (C) में से गुजरने वाली समांतर अक्ष के परितः पिंड के जड़त्व आघूर्ण (Icm) तथा उसके द्रव्यमान और दोनों समांतर अक्षों के बीच की लम्बवत दूरी के वर्ग के गुणनफल के योग के बराबर होता है। अर्थात
I = Icm + Ma2
जहां M पिंड का संपूर्ण द्रव्यमान तथा a दोनों पक्षों के बीच की दूरी है। इसे समांतर अक्षों की प्रमेय (theorem of parallel axes) कहते हैं।
उत्पत्ति
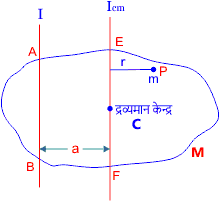
माना एक पिंड जिसका द्रव्यमान केंद्र C है इससे गुजरने वाली अक्ष EF के परितः जड़त्व आघूर्ण Icm है। अक्ष EF, अक्ष AB के समांतर है तथा इनके बीच की दूरी a है। माना अक्ष EF से r दूरी पर m द्रव्यमान का एक कण है तो इस कण की अक्ष AB से दूरी (a + r) होगी। तो
कण का EF अक्ष के परितः जड़त्व आघूर्ण = mr2
अतः संपूर्ण पिंड का EF अक्ष के परितः जड़त्व आघूर्ण
Icm = Σmr2
एवं संपूर्ण पिंड का AB अक्ष के परितः जड़त्व आघूर्ण
I = Σm(r + a)2
I = Σm(r2 + a2 + 2ra)
I = Σmr2 + Σma2 + Σm(2ra)
चूंकि a नियत है इसलिए इसे Σ से बाहर ले सकते हैं
I = Σmr2 + a2Σm + 2aΣmr
अब Icm = Σmr2 है तो
I = Icm + a2Σm + 2aΣmr
चूंकि द्रव्यमान केंद्र के परितः Σmr = 0 एवं Σm = M है तब
\footnotesize \boxed { I = I_cm + Ma^2 }
यही जड़त्व आघूर्ण संबंधी समांतर अक्ष की प्रमेय हैं।
पढ़ें… 11वीं भौतिक नोट्स | 11th class physics notes in Hindi
2. लम्ब अक्षों की प्रमेय
किसी समतल पटल का उसके तल में ली गई परस्पर दो अक्षों OX तथा OY के परितः जड़त्व आघूर्ण का योग, इन अक्षों के कटान बिंदु O से जाने वाली तथा समतल पटल के लंबवत अक्ष OZ के परितः जड़त्व आघूर्ण के बराबर होता है अर्थात
IX + IY + IZ
जहां IX तथा IY पटल की अक्ष OX व OY के परितः जड़त्व आघूर्ण है इसे लम्ब अक्षों की प्रमेय (theorem of perpendicular axes) कहते हैं।
उत्पत्ति

माना समतल पटल के तल में दो परस्पर लंबवत अक्ष OX व OY हैं। चित्र में P बिंदु पर पिंड का एक कण है जिसका द्रव्यमान m है एवं इसकी कटान बिंदु से दूरी r है तो
पूरे पटल का OX अक्ष के परितः जड़त्व आघूर्ण IX = Σmy2
इसी प्रकार पटल का OY अक्ष के परितः जड़त्व आघूर्ण IY = Σmx2
अतः OZ अक्ष के परितः पूरे पटल का जड़त्व आघूर्ण
IZ = Σmr2
IZ = Σm(x2 + y2) (चूंकि r2 = x2 + y2)
IZ = Σmx2 + Σmy2
अतः Σmx2 तथा Σmy2 के मान रखने पर
IZ = IY + IX
\footnotesize \boxed { I_Z = I_X + I_Y }
यही जड़त्व आघूर्ण संबंधी लम्ब अक्षों की प्रमेय हैं।