टाॅरिसेली प्रमेय
इस नियम के अनुसार, किसी द्रव से भरी टंकी की दीवार पर एक सूक्ष्म छिद्र कर दिया जाता है तो इसमें से निकलने वाले द्रव का बहि:स्त्राव वेग, द्रव की मुक्त सतह से छिद्र तक गुरुत्व के अधीन गिरने वाले तथा पिंड द्वारा प्राप्त किए गए वेग के बराबर होता है इसे टाॅरिसेली प्रमेय कहते हैं। या टाॅरिसेली प्रमेय नियम भी कह सकते हैं।
वैज्ञानिक टाॅरिसेली ने बताया कि जब किसी द्रव से भरी टंकी में हम उसकी सतह से ऊपर एक छिद्र कर दें तो द्रव उस छिद्र में जिस वेग से नीचे गिरता है उस वेग को बहि:स्त्राव वेग कहते हैं।
सूत्र की उत्पत्ति
माना एक पात्र है जिसमें H ऊंचाई तक द्रव भरा है पात्र (टंकी) के ऊपरी स्वतंत्र तल से h गहराई पर एक छिद्र है। माना पात्र के स्वतंत्र तल और छिद्र पर वायुमंडलीय दाब उपस्थित है। तो द्रव के प्रवाह पर इस दाब का कोई प्रभाव नहीं पड़ेगा। अर्थात स्वतंत्र तल पर गतिज ऊर्जा शून्य होगी।
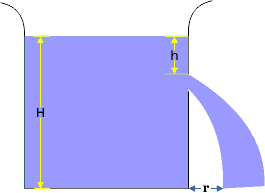
माना द्रव का घनत्व ρ तथा वायुमंडलीय दाब P है एवं द्रव, छिद्र से v बहि:स्त्राव वेग से बाहर निकल रहा है। द्रव के बहि:स्त्राव वेग v तथा स्वतंत्र तल से छिद्र की दूरी h में निम्न संबंध होगा।
बरनौली प्रमेय के अनुसार, द्रव के स्वतंत्र तल पर तथा छिद्र के हर एक बिंदु पर द्रव का दाब तथा एकांक आयतन का कुल दाब का योग बराबर होना चाहिए। अतः
P + 0 + ρgH = P + \large \frac{1}{2} ρv2 + ρg(H – h)
ρgH = \large \frac{1}{2} ρv2 + ρgH – ρgh
ρgh = \large \frac{1}{2} ρv2
v2 = 2gh
\footnotesize \boxed { v = \sqrt{2gh} }
इस समीकरण को ही बहि:स्त्राव वेग का नियम कहते हैं।
जहां v बहि:स्त्राव वेग , h स्वतंत्र तल से छिद्र तक की गहराई तथा g गुरुत्वीय त्वरण है।
पढ़ें… 11वीं भौतिक नोट्स | 11th class physics notes in Hindi
अर्थात् इस समीकरण द्वारा स्पष्ट होता है कि किसी छिद्र से गिरते द्रव का बहि:स्त्राव वेग v , छिद्र की द्रव के स्वतंत्रत तल से गहराई h तथा उसके गुरुत्वीय त्वरण g के दोगुने के गुणनफल के वर्गमूल के बराबर होता है।
इस सूत्र द्वारा यह भी स्पष्ट होता है पात्र में द्रव स्वतंत्र तल से क्षेत्र जितनी अधिक गहराई पर होता है द्रव का का मान उतना ही अधिक होता है वही श्वाबे कमांड रब की आकृति उसकी मात्रा और छिद्र के आकार पर भी निर्भर करता है।