इस अध्याय के अंतर्गत सदिशों के योग का त्रिभुज नियम समझाया गया है। यह पूर्ण रूप से चित्र द्वारा वर्णित किया गया है यह त्रिभुज नियम कभी-कभी Long questions में आ जाता है। इसलिए आप इसे समझें और लिखकर अभ्यास करें।
सदिशों के योग का त्रिभुज नियम
इस नियम के अनुसार, यदि दो सदिशों को परिमाण व दिशा में किसी त्रिभुज की दो क्रमागत भुजाओं से निरूपित किया जाता हो, तब इन सदिशों का परिणामी, परिमाण व दिशा में विपरीत क्रम में ली गई त्रिभुज की तीसरी भुजा के द्वारा निरूपित होगा। इसे सदिशों के योग का त्रिभुज नियम कहते हैं।
पढ़ें.. सदिशों के योग का समांतर चतुर्भुज नियम
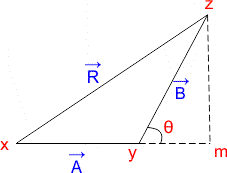
माना दो सदिश \overrightarrow{A} व \overrightarrow{B} हैं जिनका परिमाण व दिशा में ∆xyz की दो क्रमागत भुजाओं \overrightarrow{xy} व \overrightarrow{yz} द्वारा निरूपित है।
तब इन सदिशों का परिणामी \overrightarrow{R} त्रिभुज की तीसरी भुजा xz द्वारा प्रदर्शित किया जाएगा चित्र में स्पष्ट किया गया है।
अब तीसरी भुजा का परिणामी \overrightarrow{R} का परिमाण R ज्ञात करेंगे।
इसके लिए भुजा xy को आगे बढ़ाकर m तक ले जाते हैं जो कि ∆ के बिंदु z से डाला गया लंब का कार्य करती है।
माना ∠zym = θ हो तब ∆xzm में
(कर्ण)2 = (लंब)2 + (आधार)2
(xz)2 = (zm)2 + (xm)2
(xz)2 = (zm)2 + (xy + ym)2 (चूंकि xm=xy+ym)
(xz)2 = (zm)2 + (xy)2 + (ym)2 + 2(xy)(ym)
चूंकि ∆yzm में (zm)2 + (ym)2 = (yz)2 है तब
(xz)2 = yz2 + xy2 + 2(xy)(ym) समी.①
समकोण ∆yzm में
cosθ = आधार/कर्ण = ym/yz
तथा ym = yz cosθ
ym का मान समी.① में रखने पर
xz2 = yz2 + xy2 + 2(xy)(yz cosθ)
चूंकि शुरू में ही पढ़ा था कि xz = R, xy = A तथा yz = B है तब उपरोक्त समीकरण
R2 = A2 + B2 + 2ABcosθ
दोनों ओर वर्गमूल करने पर
\footnotesize \boxed { R = \sqrt{A^2 + B^2 + 2ABcosθ} }
अतः इस समीकरण द्वारा दो क्रमागत भुजाओं के मान से उनका परिणाम का परिमाण ज्ञात किया जा सकता है।
पढ़ें… 11वीं भौतिक नोट्स | 11th class physics notes in Hindi
अब परिणामी \overrightarrow{R} की दिशा ज्ञात करने के लिए सदिश \overrightarrow{A} पर एक कोण बनाते हैं।
तो ∆xmz में
tanα = लंब/आधार = zm/xm = zm/(xy + ym)
अब चूंकि ऊपर xy = A, ym = yz cosθ तथा zm = yzsinθ होगा। तो
\footnotesize \boxed { tanα = \frac{Bsinθ}{A + Bcosθ} }
यही सदिश योग के त्रिभुज नियम का सूत्र है।
New Notes in Physics