एंपीयर के परिपथीय नियम के अनुप्रयोग
एंपीयर के परिपथ नियम के अनुप्रयोग को विभिन्न भागों में बांटा गया है। जिसमें से दो भागों के बारे में हम इस अध्याय में पढ़ेंगें।
1. धारावाही परिनालिका के अंदर चुंबकीय क्षेत्र ज्ञात करना
परिनालिका एक लंबी बेलनाकार कुंडलिनी (helix) होती है। तथा इसमें i एंपियर की धारा प्रवाहित हो रही है।
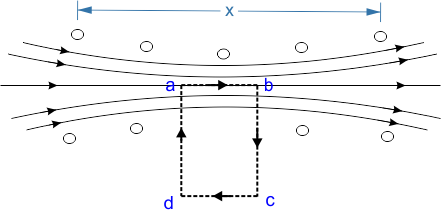
माना एक आयताकार बंद परिपथ abcd है। यदि परिनालिका के प्रति मीटर लंबाई में फेरो (लपेटो) की संख्या n है। तथा इसमें i एंपियर की धारा बह रही है। तो इस आयताकार परिपथ abcd पर एंपीयर का परिपथ नियम लगाने से
\oint \overrightarrow{B} • \overrightarrow{dℓ} = µ_0\,i
आयताकार बंद परिपथ abcd के लिए
\small \oint \overrightarrow{B} • \overrightarrow{dℓ} = \small \int^b_a \overrightarrow{B} • \overrightarrow{dℓ} + \small \int^c_b \overrightarrow{B} • \overrightarrow{dℓ} + \small \int^d_c \overrightarrow{B} • \overrightarrow{d} + \small \int^a_d \overrightarrow{B} • \overrightarrow{dℓ}
आयताकार लूप abcd के लिए bc तथा da चुंबकीय क्षेत्र के लंबवत् हैं। अतः θ = 90° होने पर परिणामी शून्य होगा। अर्थात्
\small \int^c_b \overrightarrow{B} • \overrightarrow{dℓ} = \small \int^a_d \overrightarrow{B} • \overrightarrow{dℓ}
\small \int^c_b \overrightarrow{B} • \overrightarrow{dℓ} = Bdℓ cos90°
\small \int^c_b \overrightarrow{B} • \overrightarrow{dℓ} = 0
अब cd, परिनालिका के बाहर है। इसलिए चुंबकीय क्षेत्र का मान लगभग सुनने होगा
इस प्रकार कुल चुंबकीय क्षेत्र
\small \oint \overrightarrow{B} • \overrightarrow{dℓ} = \small \int^b_a \overrightarrow{B} • \overrightarrow{dℓ}
\small \oint \overrightarrow{B} • \overrightarrow{dℓ} = \small \int^b_a B dℓ cos0°
\small \oint \overrightarrow{B} • \overrightarrow{dℓ} = B \small \int^b_a dℓ
\small \oint \overrightarrow{B} • \overrightarrow{dℓ} = Bx समी.
जहां x संपूर्ण लंबाई है।
अब माना परिनालिका की प्रति एकांक लंबाई में फेरों की संख्या n है। तब x लंबाई में फेरों की संख्या nx होगी। प्रत्येक फेरे में धारा io है। तो पथ द्वारा कुल घिरी कुल धारा nxio है। अर्थात
कुल धारा = nxio
एंपियर के नियमानुसार
\small \oint \overrightarrow{B} • \overrightarrow{d} = µ_0\,i
अब समी. से \small \oint \overrightarrow{B} • \overrightarrow{dℓ} का मान रखने पर
Bx = µ0i
तथा Bx = µ0nxi
\footnotesize \boxed { B = µ_0\,n\,i } टेस्ला
पढ़ें… 12वीं भौतिकी नोट्स | class 12 physics notes in hindi pdf
2. धारावाही टोराॅइट के कारण चुंबकीय क्षेत्र
एक ऐसा वृत्ताकार छल्ला, जिस पर किसी चालक तार के अनेकों फेरे समीप-समीप लिपटे होते हैं। इस धारावाही वृत्ताकार छल्ले को टोराॅइट कहते हैं।
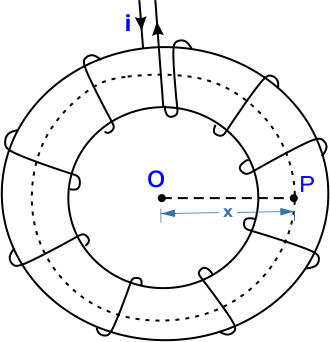
माना टोराॅइट की कोर (core) के अंदर बिंदु P से होकर जाने वाले वृत्ताकार पथ की त्रिज्या x है। टोराॅइट के किसी बिंदु P पर चुंबकीय क्षेत्र ज्ञात करना है। तो एंपियर के नियम से
\oint \overrightarrow{B} • \overrightarrow{dℓ} = µ_0\,i
जहां i टोराॅइट की कुल धारा है।
चुंबकीय क्षेत्र \overrightarrow{B} तथा \overrightarrow{dℓ} प्रत्येक बिंदु पर एक ही दिशा में होंगे। तब
\small \oint \overrightarrow{B} • \overrightarrow{dℓ} = \int B dℓ cos0°
\small \oint \overrightarrow{B} • \overrightarrow{dℓ} = B \int dℓ
\oint \overrightarrow{B} • \overrightarrow{dℓ} = B(2πx) समी.
वृत्ताकार पथ में फेरों की संख्या n है। अतः पूरी टोराॅइट में फेरों की संख्या n × 2πx होगी। इस प्रकार वृत्तीय पथ द्वारा कुल धारा n × 2πx × i होगी। तो
\small \oint \overrightarrow{B} • \overrightarrow{d} = µ_0\,i
अब समी. से तथा i का मान उपरोक्त समीकरण में रखने पर
B(2πx) = µ0 × n × 2πx × i
अब चुंबकीय क्षेत्र
\footnotesize \boxed { B = µ_0\,n\,i } टेस्ला
Nice notes