चुंबकीय क्षेत्र की परिभाषा | एक समान चुंबकीय क्षेत्र में आवेशित कण की गति

चुंबकीय क्षेत्र की परिभाषा

किसी चुंबकीय के चारों ओर का वह क्षेत्र जिसमें कोई चुंबकीय सुई एक बल का अनुभव करती है। इस बल कारण चुंबकीय सुई एक निश्चित दिशा में ठहरती है। चुंबक के चारों ओर कि इसी क्षेत्र को चुंबकीय क्षेत्र कहते हैं।
चुंबकीय सुई जिस दिशा में ठहरती है वही चुंबकीय क्षेत्र भी दिशा होती है।

एक समान चुंबकीय क्षेत्र में आवेशित कण की गति

एक समान चुंबकीय क्षेत्र में आवेशित कण तीन प्रकार से गति कर सकता है।

1. चुंबकीय क्षेत्र के समान्तर

चुंबकीय क्षेत्र में लगने वाला बल
F = qVBsinθ

जब आवेशित कण चुंबकीय क्षेत्र में समांतर प्रवेश करता है।
तब   θ = 0 तो
F = qVBsinθ
\footnotesize \boxed { F = 0 }

अर्थात् जब आवेशित कण चुंबकीय क्षेत्र के समांतर प्रवेश करता है। तो इस पर कोई कार्य नहीं होता है।
यह भी पढ़ें… विद्युत धारा के नोट्स

2. चुंबकीय क्षेत्र के लंबवत

माना +q आवेश का एक आवेशित कण है। जो एक समान चुंबकीय क्षेत्र B में V वेग से क्षेत्र की दिशा के लंबवत प्रवेश करता है। तो इस आवेशित कण पर लगने वाला लॉरेंज बल

F = qVB समी. ①

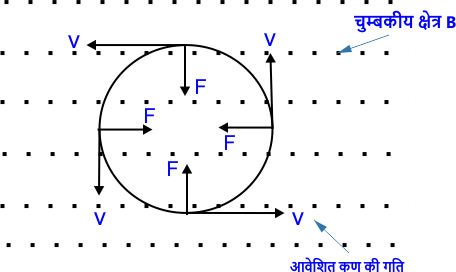
(यहां चित्र में point से चुंबकीय क्षेत्र को दर्शाया गया है।)
इस बल की दिशा फ्लेमिंग के बाएं हाथ के नियम के
अनुसार चुंबकीय क्षेत्र तथा कण की गति दोनों के लंबवत होगी। जिसके कारण आवेशित कण एक वृत्तीय पथ पर गति करने लगेगा।
यदि आवेशित कण का द्रव्यमान m त्रिज्या r है। तो वृत्ताकार पथ पर लगने वाला अभिकेंद्र बल

F = \large \frac{mv^2}{r}   समी. ②
अब समी. ① व समी. ② को बराबर रखने पर
F = F
qvB = \large \frac{mv^2}{r}
\footnotesize \boxed { r = \frac{mv}{qB} }
यदि आवेशित कण का संवेग है। तो P (= mv ) है। तो
\footnotesize \boxed { r = \frac{P}{qB} }

इस सूत्र से स्पष्ट है। कि वृत्ताकार पथ की त्रिज्या r, आवेशित कण के संवेग P के अनुक्रमानुपाती होती है।
यदि कण की गतिज ऊर्जा k हो तो

K = \large \frac{1}{2} mv^2
या     v = \sqrt{ \frac{2k}{m} }
तब v का मान उपरोक्त समीकरण में रखने पर
r = \large \frac{mv}{qB}
r = \large \frac{m×\sqrt{2k/m}}{qB}
r = \large \frac{\sqrt{2k/m^2}}{qB}
\footnotesize \boxed { r = \frac{\sqrt{2mk}}{qB} }

Note – यदि आवेश चुंबकीय क्षेत्र में तिरछा प्रवेश करता है। तो उसका पथ एक कुण्डलिनी (helix) के रूप में होगा

एक वृत्ताकार चक्कर पूरा करने में आवेशित कण द्वारा क्षेत्र की दिशा में चली गई दूरी को पिच (pich)कहते हैं। वृत्ताकार पथ का आवर्तकाल

\footnotesize \boxed { T = \frac{2πm}{qB} }