संधारित्र का संयोजन
अनेक प्रयोगों में धारिता में परिवर्तन करने के लिए दो या दो से अधिक संधारित्रों को एक साथ जोड़ना पड़ता है। संधारित्रों को जोड़ने के दो संयोजन (क्रम) है।
(i) श्रेणीक्रम संयोजन (ii) समांतर क्रम संयोजन
संधारित्र का श्रेणीक्रम संयोजन
श्रेणीक्रम संयोजन में पहले संधारित्र की दूसरी प्लेट को दूसरे संधारित्र की पहली प्लेट से तथा दूसरे संधारित्र की दूसरी प्लेट को तीसरे संधारित्र की पहली प्लेट से जोड़ते हैं। और यदि ज्यादा संधारित्र हैं, तो आगे भी इसी क्रम में जोड़ते हैं। संधारित्र के इस संयोजन को श्रेणीक्रम संयोजन कहते हैं। चित्र से स्पष्ट है।
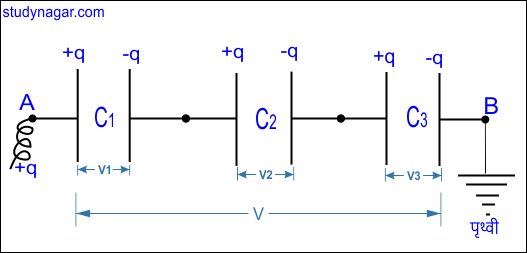
माना तीन संधारित्र C1, C2 व ,C3 श्रेणी क्रम में बिंदुओं A और B के बीच जोड़े गए हैं। तो संधारित्र की सभी प्लेटों पर समान आवेश होगा जबकि सभी प्लेटों के बीच विभवांतर क्रमशः V1, V2 व V3 होंगे।
तो V1 = \large \frac{q}{C_1} , V2 = \large \frac{q}{C_2} तथा V3 = \large \frac{q}{C_3}
अब बिंदुओं A और B के बीच कुल विभवांतर
V = V1 + V2 + V3
V = \large \frac{q}{C_1} + \large \frac{q}{C_2} + \large \frac{q}{C_3} – समीं. ①
यदि बिंदुओं A और B के बीच तुल्य धारिता C हो तो
V = \large \frac{q}{C} – समीं. ②
अब समीं. ① से V का मान समीं. ② में रखने पर
\large \frac{q}{C} = \large \frac{q}{C_1} + \large \frac{q}{C_2} + \large \frac{q}{C_3}
\large \frac{q}{C} = q\large( \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3})
\footnotesize \boxed{ \frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}}
स्पष्ट है कि तीन या अधिक संधारित्र श्रेणीक्रम में जुड़े हैं। तो उनकी तुल्य धारिता का व्युत्क्रम, तीनों संधारित्रों की अलग-अलग धारिताओं के व्युत्क्रम के योग के बराबर होता है। श्रेणी क्रम में जुड़े सभी संधारित्र पर आवेश की मात्रा समान होती है।
यह भी पढ़ें… विलगित गोलीय चालक की धारिता
संधारित्र का समांतर क्रम संयोजन
समांतर क्रम संयोजन में सभी संधारित्रों को एक साथ जोड़ने के लिए उन सभी संधारित्रों की पहली प्लेट को एक बिंदु A से जोड़ देते हैं। तथा सभी संधारित्रों की दूसरी प्लेट को दूसरे बिंदु B से जोड़ देते हैं। और यदि कई संधारित है। तो उन्हें भी इसी क्रम में जोड़ते हैं। तो संधारित्र के इस संयोजन को समांतर क्रम संयोजन कहते हैं। चित्र से स्पष्ट है।
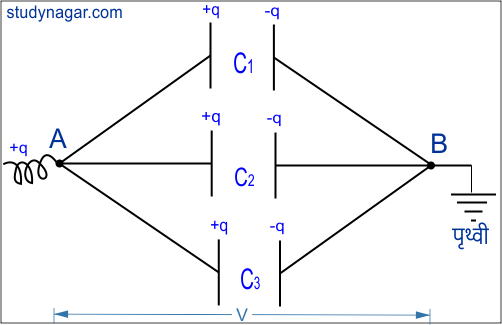
माना तीन संधारित्र C1, C2 व ,C3 समांतर क्रम में बिंदुओं A और B के बीच जोड़े गए हैं। तो संधारित्रों पर विभवांतर समान होगा। जबकि इन पर आवेश क्रमशः q1, q2 व q3 होंगे।
तो q1 = C1V, q2 = C2V तथा q3 = C3V
अतः आवेश के संरक्षण से
q = q1 + q2 + q3
q = C1V + C2V + C3V – समीं. ①
यदि बिंदुओं A और B के बीच तुल्य धारिता C है तो
q1 = CV – समीं. ②
अब समीं. ① से q का मान समीं. ② में रखने पर
CV = C1V + C2V + C3V
CV = V(C1 + C2 + C3)
\footnotesize \boxed{ C = (C_1 + C_2 + C_3) }
पढ़ें… 12वीं भौतिकी नोट्स | class 12 physics notes in hindi pdf
स्पष्ट है कि तीन या अधिक संधारित्र समांतर क्रम में जुड़े हैं। तो उनकी तुल्य धारिता, तीनों संधारित्रों की अलग-अलग धारिताओं के योग के बराबर होता है। समांतर क्रम में जुड़े सभी संधारित्र पर विभवांतर समान होता है।
यह भी पढ़ें… संधारित्र का सिद्धांत क्या है

