स्थिर विद्युत विभव तथा धारिता | Physics class 12 chapter 2 notes in hindi pdf

Physics class 12 chapter 2 notes in hindi pdf

इस पोस्ट में स्थिर विद्युत विभव तथा धारिता Physics class 12 chapter 2 के सभी टॉपिक को एक notes के रूप में हिन्दी में तैयार किया गया है। और pdf भी जल्द ही आ जायेगी।

विद्युत विभव

एकांक आवेश को अनंत से विद्युत क्षेत्र के भीतर किसी बिंदु P तक लाने में किए गए कार्य को उस बिंदु पर विद्युत विभव कहते हैं।

यदि किसी परीक्षण आवेश q₀ को अनंत से ‌विद्युत क्षेत्र के भीतर किसी बिंदु P तक लाने में किया गया कार्य W है। तो उस बिंदु पर विद्युत विभव
\footnotesize \boxed { V = \frac{W}{q_0}}
इसका मात्रक जूल/कूलाम अथवा वोल्ट होता है। तथा विमीय सूत्र [ML²T^-3A^-1] है। एवं यह एक अदिश राशि है।

विद्युत विभवान्तर

किसी परीक्षण आवेश को विद्युत क्षेत्र के भीतर एक बिंदु से दूसरे बिंदु तक ले जाने में किए गए कार्य तथा परीक्षण आवेश को उन बिंदुओं के बीच विद्युत विभवान्तर कहते हैं।
यदि यह बिंदु A और B हैं तो
        \footnotesize \boxed { V_A - V_B = \frac{W}{q_0}}

इलेक्ट्रॉन वोल्ट

एक इलेक्ट्रॉन वोल्ट वह ऊर्जा है। जो कि कोई इलेक्ट्रॉन एक वोल्ट विभवान्तर द्वारा त्वरित होने पर अर्जित करता है।

पढ़ें… 12वीं भौतिकी नोट्स | class 12 physics notes in hindi pdf

विभव प्रवणता

विद्युत क्षेत्र में दूरी के सापेक्ष विभव परिवर्तन की दर को विभव प्रवणता कहते हैं।
      \footnotesize \boxed { विभव \, प्रवणता = \frac{dv}{dx}}
इसका मात्रक वोल्ट/मीटर अथवा न्यूटन/कूलाम होता है। यह एक सदिश राशि है। जिसकी दिशा निम्न विभव से उच्च विभव की ओर होती है।

बिंदु आवेश के कारण किसी बिंदु पर विद्युत विभव

सम्बन्धित प्रशन –
Q.1 बिंदु आवेश के कारण किसी बिंदु पर विद्युत विभव के लिए व्यंजक प्राप्त कीजिए?
Q.2 बिंदु आवेश के कारण किसी बिंदु पर विद्युत विभव के सूत्र V = \large \frac{1}{4πԐ_0} \frac{q}{r} का निगमन कीजिए।

हल- माना बिंदु O पर +q कूलाम आवेश स्थित है। इससे r दूरी पर एक बिंदु P है। जिस पर विद्युत विभव ज्ञात करना है।

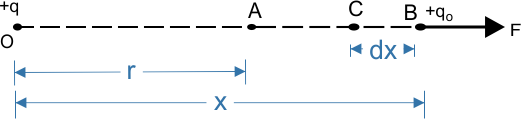
इसके लिए बिन्दु A से अनंत तक की दूरी को छोटे-छोटे भागों में बांटा गया है। यदि कोई परीक्षण आवेश +q_o बिंदु B पर स्थित है। तो उस पर लगने वाला विद्युत बल
F = \large \frac{1}{4πԐ_0} \frac{q\,q_o}{x^2}

अब परीक्षण आवेश +q_o को B से C तक लाने में किया गया कार्य
dW = F×(-dx) ⇒ \large \frac{1}{4πԐ_0} \frac{q\,q_o}{x^2}×(-dx)
dw = F×(-dx) ⇒ \large \frac{q\,q_o}{4π_0} [\frac{-dx}{x^2}]

परीक्षण आवेश +q_o को अनंत से A तक लाने में किया गया कुल कार्य
W = \large \int_{∞}^{r} \frac{q\,q_o}{4π0} [\frac{-dx}{x^2}]

W = \large \frac{q\,q_o}{4πԐ_0} \int_{∞}^{r} - \frac{1}{x^2}dx

W = \large \frac{q\,q_o}{4πԐ_0} [\frac{1}{x}]_{∞}^{r}     { समाकलन से xⁿ = \large \frac{x^{n+1}}{n+1} }
W = \large \frac{q\,q_o}{4πԐ_0} [\frac{1}{r} - \frac{1}{∞} ]
W = \large \frac{1}{4πԐ_0} \frac{q\,q_o}{r}
बिंदु A पर विभव   V = \large \frac{W}{q_o}
V = \large\frac { \frac{1}{4πԐ_0} \frac{q\,q_o}{r}}{q_o}
\footnotesize \boxed { V = \frac{1}{4πԐ_0} \frac{q}{r}} वोल्ट

इसे भी पढ़ें.. chapter 2 स्थिर विद्युत विभव तथा धारिता के प्रशन

समविभव पृष्ठ

विद्युत क्षेत्र में स्थित एक ऐसा पृष्ठ जिसके सभी बिंदुओं पर विद्युत विभव समान होता है। समविभव पृष्ठ कहलाता है। समविभव पृष्ठ के एक बिंदु से दूसरे बिंदु तक किसी आवेश को ले जाने में कोई कार्य नहीं होता है।
अर्थात्       \footnotesize \boxed { W = 0 }

आवेशों के किसी निकाय की विद्युत स्थितिज ऊर्जा

आवेशों के किसी निकाय की विद्युत स्थितिज ऊर्जा उस कार्य के बराबर होती है। जो उन आवेशों को अनंत से उनकी स्थितियों तक लाने में किया जाता है।

माना एक निकाय AB दो आवेशों +q₁ व +q₂ से मिलकर बना है। इनके बीच की दूरी r है। माना आवेश +q₂ बिंदु B पर न होकर अनंत पर है। तो आवेश +q₁ के कारण बिंदु B पर विद्युत विभव

V = \large \frac{1}{4πԐ_0} \frac{q_1}{r}       समी.①
अब आवेश +q₂ को अनंत से बिंदु B तक लाने में किया गया कार्य
W = q₂V
W = q₂\large( \frac{1}{4πԐ_0} \frac{q_1}{r} )      समी.① से
W = \large \frac{1}{4πԐ_0} \frac{q_1\,q_2}{r}
यह कार्य ही विद्युत स्थितिज ऊर्जा U है
\footnotesize \boxed { U = \frac{1}{4πԐ_0} \frac{q_1\,q_2}{r} }    जूल
Note – यदि कोई निकाय तीन आवेशों से मिलकर बना है तो उस निकाय की स्थितिज ऊर्जा
U = U₁ + U₂ + U₃
\footnotesize \boxed { U = \frac{1}{4πԐ_0} [\frac{q_1\,q_2}{r_1}+\frac{q_3\,q_4}{r_2}+\frac{q_5\,q_6}{r_3}] }

यह भी पढ़े.. विद्युत द्विध्रुव के कारण विद्युत विभव

एक समान विद्युत क्षेत्र में विद्युत द्विध्रुव को घुमाने में किया गया कार्य

सम्बन्धित प्रशन –
Q.1 एक समान विद्युत क्षेत्र में विद्युत द्विध्रुव को घुमाने में किये गये कार्य का व्यंजन ज्ञात कीजिए।

उत्तर- माना एक विद्युत द्विध्रुव क्षेत्र के समांतर AB स्थिति में रखा गया है। अब उसे θ कोण घुमाकर A’B’ स्थिति में लाया जाता है। तो विद्युत द्विध्रुव के आवेश +q को A’ पर तथा -q को B’ पर ले जाने में किया गया कार्य

W = +q आवेश का कार्य + (-q आवेश का कार्य)
W = qE (DA) + qE (BC)
W = qE (ℓ – ℓcosθ) + qE (ℓ + ℓcosθ)
W = qEℓ (1 – ℓcosθ) + qEl (1 + ℓcosθ)
W = 2qEℓ (1 – ℓcosθ)
W = PE (1 – ℓcosθ)       (P = 2qℓ)
\footnotesize \boxed {W = PE (1 - ℓcosθ)}

यह भी पढ़ें.. physics chapter 1 वैद्युत आवेश तथा क्षेत्र नोट्स
आशा है कि Physics class 12th chapter 2 notes in hindi स्थिर विद्युत विभव तथा धारिता के संबंध में कराए गए सभी आर्टिकल और थ्योरी परिभाषाएं आपको पसंद आई होंगे। अगर आपके मन में स्थिर वैद्युत विभव तथा धारिता से संबंधित कोई प्रश्न या कोई सुझाव हो तो हमें कमेंट के माध्यम से बता सकते हैं। हम जल्द से जल्द आपका जवाब देंगे।

फिजिक्स 12th क्लास चैप्टर 2 के कुछ टॉपिक ऐसे हैं। जिनको हमने इस अध्याय में कवर नहीं किया है। क्योंकि उनको समझाने के लिए हमने अलग से पोस्ट तैयार की है। नीचे दिए गए सभी टॉपिकों को उनके नाम के साथ लिंक लगाया गया है। जो टॉपिक पढ़ना हो तो उसके लिंक पर क्लिक कर कर वह टॉपिक को पूरा पढ़ लो।

1. वान डी ग्राफ जनित्र क्या है, Van de graaff generator in hindi, रचना, सिद्धांत और उपयोग
2. वान डी ग्राफ जनित्र का सिद्धांत | Van de graaff generator Ka Siddhant
3. धारिता किसे कहते हैं, मात्रक तथा विमीय सूत्र लिखिए, capacitance in hindi
4. विलगित गोलीय चालक की धारिता का सूत्र, Spherical conductor in hindi
5. संधारित्र की धारिता किसे कहते हैं, परिभाषित करें, प्रभावित करने वाले कारक
6. संधारित्र का संयोजन, श्रेणीक्रम संयोजन, समांतर क्रम संयोजन
7. समांतर प्लेट संधारित्र की धारिता, सूत्र, व्यंजक, parallel plate capacitor in hindi
8. संधारित्र का सिद्धांत क्या है समझाइए, principle of capacitor in Hindi